確率変数と確率分布

前回のコラムで、ちらっと正規分布について紹介しました。
今回は、分布について詳しく紹介したいと思います。
前回のコラムはこちらです。(「歪度・尖度と正規分布」)
まずはじめに、確率変数について紹介したいと思います。
確率変数
確率変数とは、確率が付与された変数のことです。
言葉だけだとわかりにくいので、コイントスを例として考えていきたいと思います。
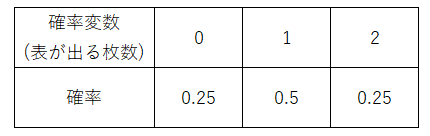
2枚のコインを投げた時、表が出た枚数は、0枚~2枚です。
組み合わせは、(表,表)、(表,裏)、(裏,表)、(裏,裏)の4通りとなります。
表が出た枚数をXとするとき、
「コイントスをして2枚とも表がでる確率」はP(X=2)=0.25と表記できます。
このときの変数Xが確率変数です。
確率分布
確率分布とは、確率変数とそのときの確率との関係を表したものです。
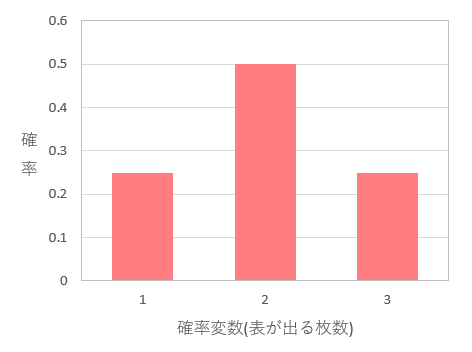
一般的に、横軸に確率変数のとる値、縦軸にそのときの確率となります。
先ほどと同様に、2枚のコインを投げた時の確率変数とそれに伴う確率について考えていきたいと思います。
これらを表とグラフにすると以下の通りになります。
まとめ
今回は、確率変数とその分布について紹介しました。
統計学において、どのような確率分布なのかを知ることはとても重要です。
前回の正規分布と合わせて覚えておくと、より深い理解につながると思います。

